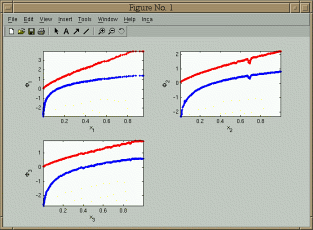
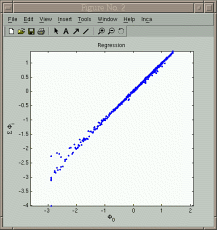
|
|||||||||||||||||||||
|
|||||||||||||||||||||

© 2004-2024 SOME RIGHTS RESERVED Please respect the copyrights! The content is protected by the Creative Commons License. If you use the provided programmes, text or figures, you have to refer to the given publications and this web site (tocsy.pik-potsdam.de) as well.
|