migram
Calculate windowed mutual information between two signals.
Syntax
i = migram(a,b,maxlag,window,noverlap,nbins)
[i,l,t] = migram(...)
i = migram(a,b)
migram(a,b)
Description
i = migram(a,b,maxlag,window,noverlap) calculates the windowed mutual information between the signals in vector a and vector b. migram splits the signals into overlapping segments and forms the columns of i with their mutual information values up to maximum lag specified by scalar maxlag. Each column of i contains the mutual information function between the short-term, time-localized signals a and b. Time increases linearly across the columns of i, from left to right. Lag increases linearly down the rows, starting at maxlag. If lengths of a and b differ, the shorter signal is filled with zeros. If n is the length of the signals, i is a matrix with 2*maxlag+1 rows and k = fix((n-noverlap)/(window-noverlap)) columns.
i = migram(a,b,maxlag,window,noverlap,nbins) calculates the mutual information based on histograms with the number of bins nbins.
i = migram(...,'norm') calculates the renormalised mutual information, which is i/log(nbins) and ensures a value range [0 1].
[i,l,t] = migram(...) returns a column of lag l and one of time t at which the mutual information is computed. l has length equal to the number of rows of i, t has length k.
i = migram(a,b) calculates windowed mutual information using defeault settings; the defeaults are maxlag = floor(0.1*n), window = floor(0.1*n), noverlap = 0 and nbins = 10. You can tell migram to use the defeault for any parameter by leaving it off or using [] for that parameter, e.g. migram(a,b,[],1000).
migram(a,b) with no output arguments plots the mutual information using the current figure.
Examples
x = cos(0:.01:10*pi)';
y = sin(0:.01:10*pi)' + .5 * randn(length(x),1);
migram(x,y)
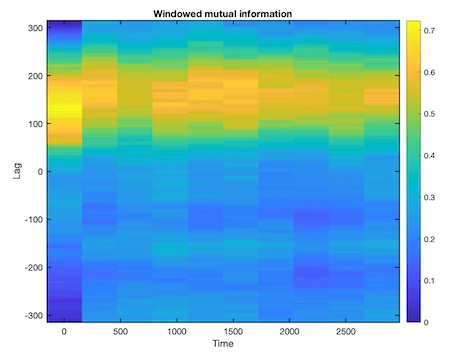
Remark
Please note that the mutual information derived with mi slightly differs from the results derived with migram. The reason is that mi also considers estimation errors. A full explanation can be found in this white paper.
 © N. Marwan, 2024
© N. Marwan, 2024