Frequently Asked Questions I. Is the software package free? II. Can I use wavelet coherency as a black box? 1. What does wavelet coherency measure? 2. What does the wavelet phase spectrum measure? 3. When should I use wavelet coherency? 4. Is the continuous global wavelet spectrum identical to the Fourier spectrum of a signal? 5. Why do I need to smooth the wavelet sample spectrum? 6. What does a peak in the cross wavelet spectrum mean? 7. Is a peak exceeding the 95% significance counter level significant on the 95% level? Question I: Is the software package free? Answer: Yes. You can download it for free according to the GNU General Public License. I just ask you to cite my website and the following two papers when you use the package: D. Maraun, J. Kurths and M. Holschneider: Nonstationary Gaussian Processes in Wavelet Domain: Synthesis, Estimation and Significance Testing. Phys. Rev. E 75, 016707, 2007 D. Maraun and J. Kurths: Cross Wavelet Analysis. Significance Testing and Pitfalls, Nonlin. Proc. Geoph. 11(4), 505-514, 2004, pdf, 282kB Question II: Can I use wavelet coherency as a black box? Answer: Well, for sure you can. But I urge you not to do it! I highly recommend to read the Chapters 1-3 and 13 in the book of Honerkamp [10] as an introduction into fundamental issues of time series analysis. To really understand the concept of wavelet spectral analysis, one should first become familiar with Fourier analysis. Good literature are e.g. [1] and [2]. I prepared a brief introduction to Cross Spectral Analysis. Finally, I recommend to read my papers or thesis [7,8,9] or at least the FAQs to get a feeling on how to interpret wavelet spectra and the common pitfalls. Question 1: What does wavelet coherency measure? Answer: Wavelet coherency is the wavelet domain equivalent to the correlation function thus measures the linear relation between two processes with respect to time and scale. A value of one implies a perfect linear relation, a value less than one occurs, when a perfect linear relation is disturbed by noise, by external influences on at least one of the processes or when the relation is not linear. Question 2: What does the wavelet phase spectrum measure? Answer: The wavelet phase spectrum estimates the phase difference of two processes with respect to time and scale. A positive value indicates a lead of the first process against the second, a negative value indicates a lag. Two interesting cases should be named explicitely: + If the second process is the time derivative of the first process (e.g. an AR1 process and its driving noise, see figure), a constant phase of -PI/2 results: 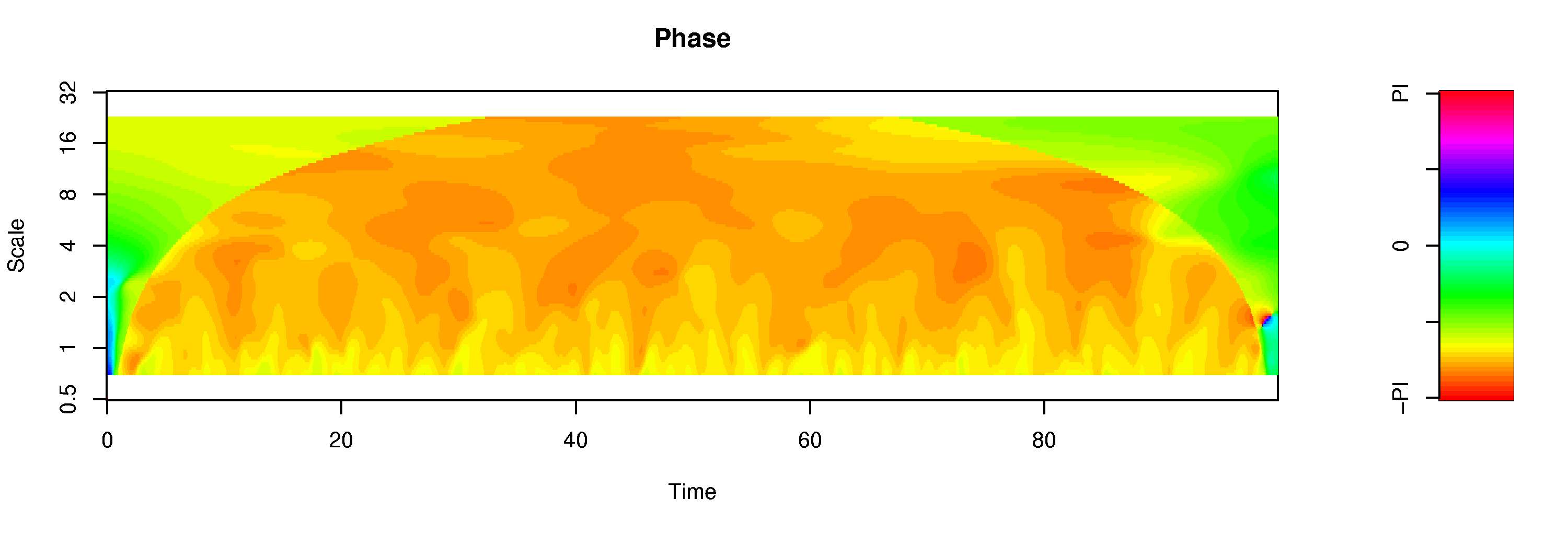+ If the second process is a time delayed version of the first process, i.e. y(t-t0) = x(t), then a time independent phase with Phi(s) = 2PI t0/s will result: 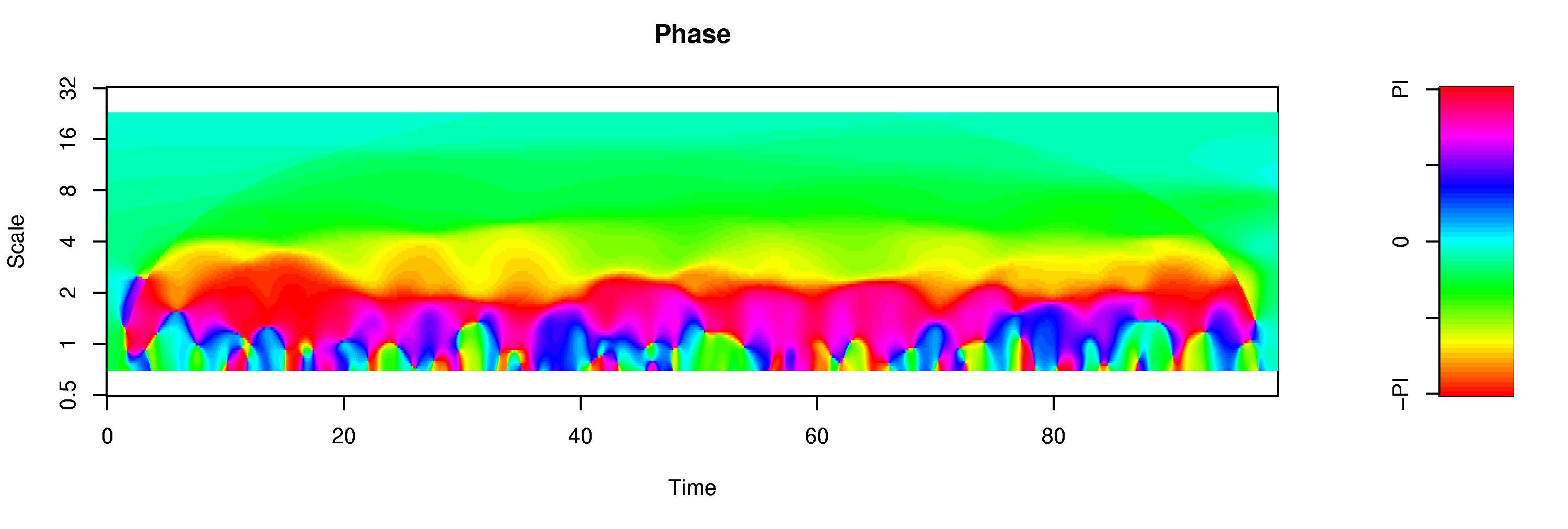Question 3: When should I use wavelet coherency? Answer: Wavelet coherency is not a magic tool to solve all bivariate problems of time series analysis. Also here the no-free-lunch-theorem holds. So, first you should answer yourself some questions: + Do I have enough data for such a sophisitcated method? E.g. 20 years of data to analyse scales from 1 to 10 years would not yield any reliable results for the long scales. + DO I REALLY NEED wavelet coherency? You should not use this tool, when you are not interested in a scale resolved analysis of a clearly nonstationary interrelation. Remember such well established and powerful tools as Fourier coherency which might do a better job. And also do not forget about correlation analysis for a first inspection! And sometimes even such freaky methods as a phase reconstruction approach might be more suitable: + If the two processes and their coherency are approximately stationary, one should better use Fourier Coherency to get uncorrelated scales and analytical error bounds or significance levels. + If the two processes perform distinct oscillations and one is interested in these relation between these oscillations, one should rather use a phase reconstruction approach to ensure the best time resolution (see Maraun and Kurths, Epochs of Phase Coherence between ENSO and Indian Monsoon, Geophys. Res. Lett., 2005) Question 4: Is the continuous global wavelet spectrum identical to the Fourier spectrum of a signal? Answer: No. In fact, the discrete global wavelet spectrum would be approximately for scale free processes. But in the continuous case things are a bit different: + Neighbouring scales are not uncorrelated. Thus a sharp peak in the Fourier spectrum will always be folded with the reproducing kernel shown in the figure (for a peak at a 2 years period and one at 8 years period). For sure one can reduce the time resolution in favour of the frequency resolution (by omega_0 in case of the Morlet wavelet), but in this case one should rather use the Fourier coherency because significance testing is much more straight forward there. 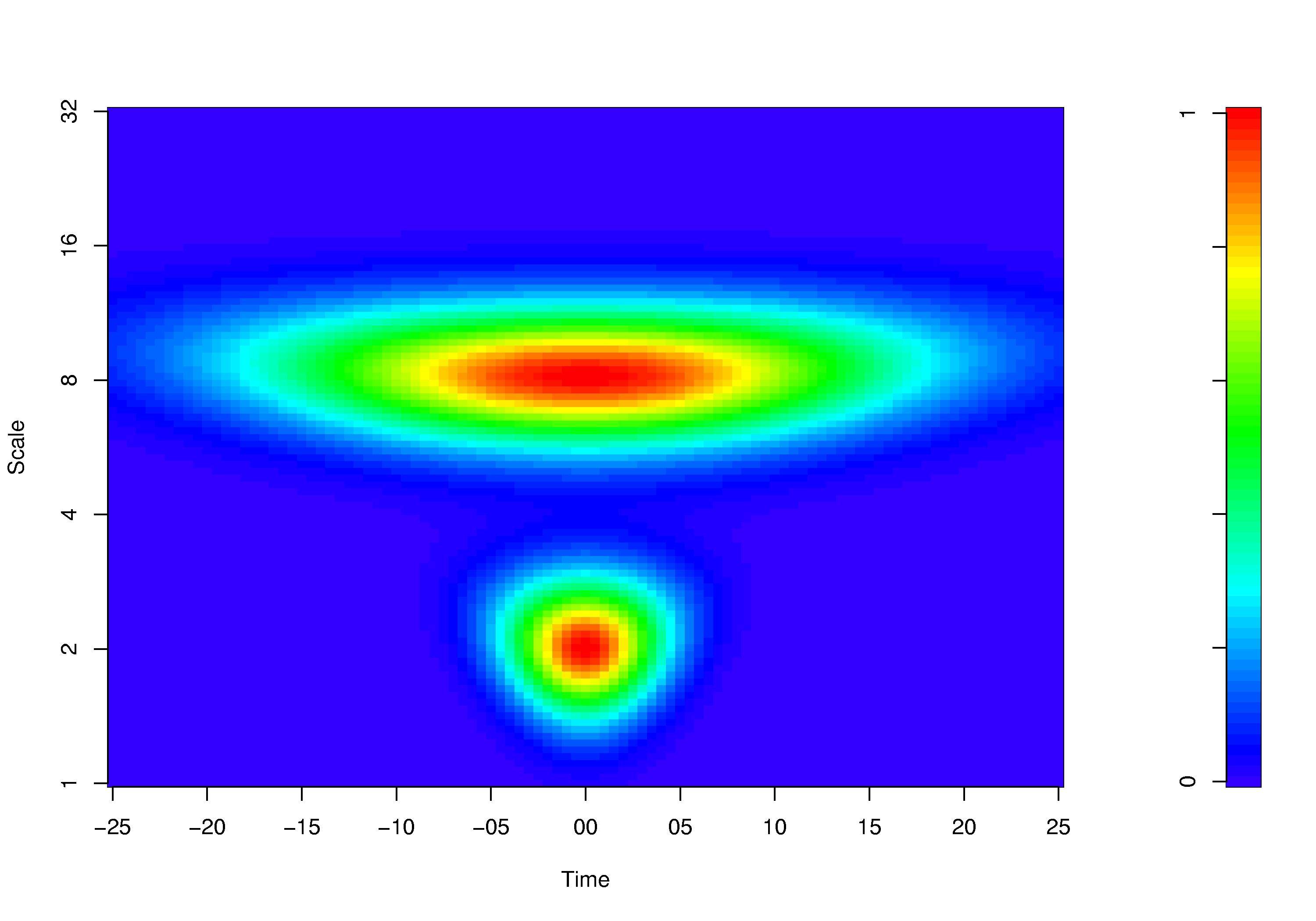Question 5: Why do I need to smooth the sample wavelet spectrum? Answer: Because all wavelet measures consider expectation values. This is because of the following reason which might at first sound a bit too theoretical and irrelevant: Coherency (as well as e.g. stationarity) might be attributed to some processes, but not to time series. Two time series might be realizations of two coherent processes, but the time series itself are not coherent. Time series analysis now tries to infer whether the time series might represent two coherent processes with a certain probability. Thats why we need significance testing and all this stuff. And because of this, a time series analyist never calculates the wavelet spectrum/coherency of time series but estimates the wavelet spectrum/coherency of the underlying processes. The wavelet periodogram (i.e. the spectrum without taking expecation values) is Chisquare distributed, i.e. having a hugh variance. To reduce the variance, one has to smooth. In the case of coherency this is essential, because otherwise the coherency is estimated to be identical to one for any two time series - even if the real coherency of the two processes is zero. Question 6: What does a peak in the cross wavelet spectrum mean? Answer: Basically: nothing. In theory, the modulus of the cross wavelet spectrum is zero when two processes are linearly independent and larger than zero, if there is some (not necessarily linear) relation. But for practical purposes, the cross wavelet spectrum is rather useless because of two reasons: + We don't know the real cross wavelet spectrum. We just have an estimator for it, the sample cross wavelet spectrum (which without smoothing is called cross wavelet periodogram or cross wavelet scalogram, following the terms of Fourier analysis). The modulus of this estimator is always larger than zero. Thus, we have to perform a significance test to judge, if the value we estimated is large enough to be significantly different from zero. + Here, the second problem arises: The cross wavelet spectrum is not normalized. Thus, in practice (because the estimated cross wavelet spectrum is not zero even for independent processes), a peak in the estimated modulus of the cross wavelet spectrum appears in three cases: either the first processes exhibits a peak, or the second process or both. But it doesn't tell us, what case we observe. So, a peak might just mean, that one of the processes exhibits high power, even if there is no relation to the other process. A plot of the estimated cross wavelet spectrum between the NINO3 index and white noise illustrates this: 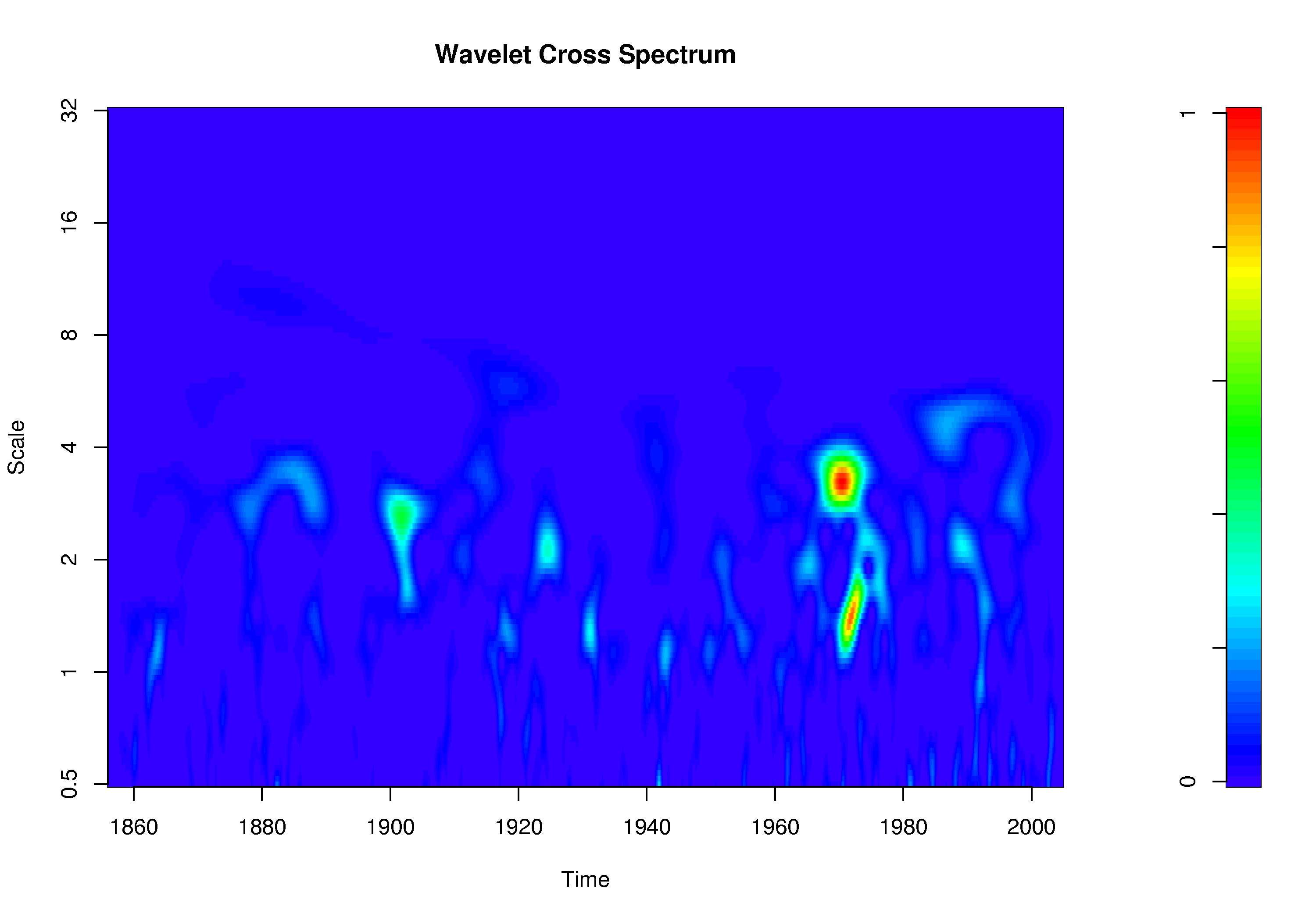Both processes are independent by definition. However, for every large El Nino, a peak occurs. Thus, I also think that it is meaningless to perform any significance test for the cross wavelet spectrum. What would be the null hypothesis? If one really knew the expectation values, this problem would not occur, but this is rather impossible in practical considerations. Wavelet coherency normalizes to the power of the single processes and thus avoids misinterpretations to a great extend. Question 7: Is a peak exceeding the 95% significance counter level significant on the 95% level? Answer: Not necessarily. And if it is small: Probably not. Due to multiple testing, spurious peaks have to appear by definition. This might be illustrated by a plot showing the estimated coherency between two independent white noise processes: 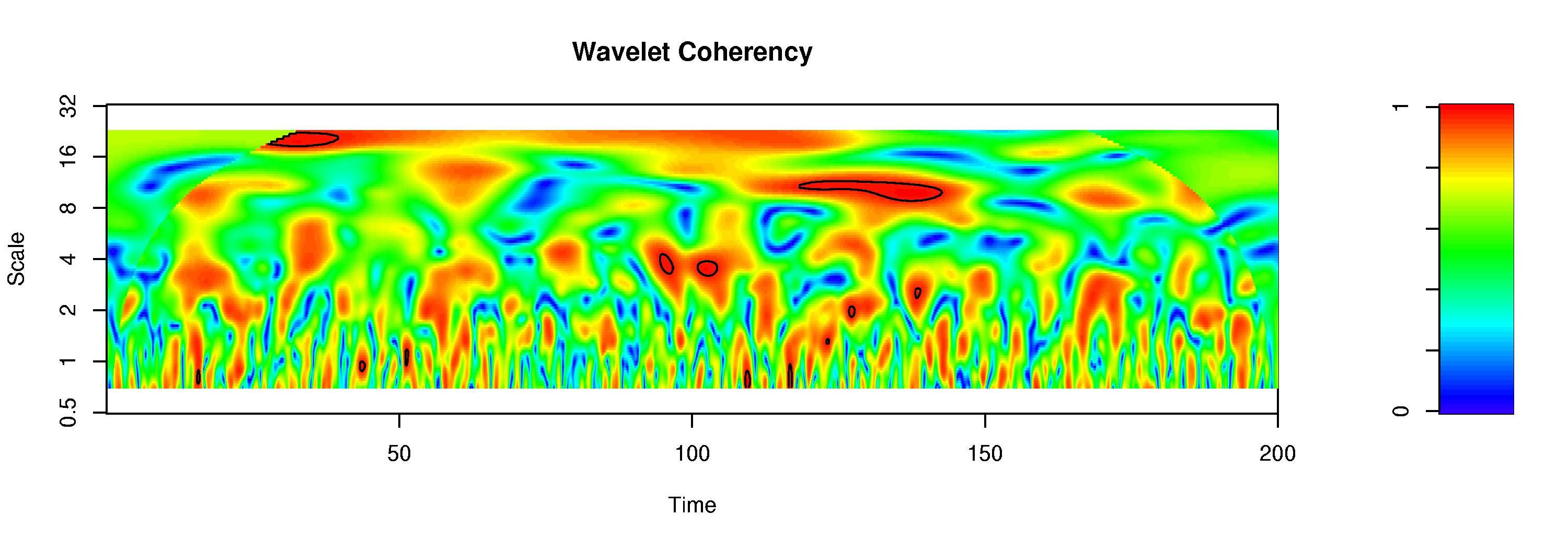The size of spurious peaks is related to the reproducing kernel, i.e. intrinsic correlations between neighbouring scales and times, which are a function of scale. Thus, the peak size should give some information whether a peak is large enough to be significant on the scale considered. The areawise significance test accounts for this problem.